Semejanza de triángulos

Dos triángulos son semejantes si cumplen alguna de las siguientes propiedades:

a) Todos sus lados son proporcionales

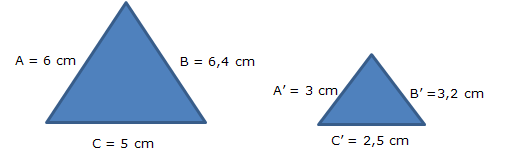
Vemos que los lados del ejemplo guardan la misma proporción:

Lado A / Lado A’ = 6 / 3 = 2
Lado B / Lado B’ = 6,4 / 3,4 = 2
Lado C / Lado C’ = 5 / 2,5 = 2

b) Tienen los tres ángulos iguales

Estos dos ángulos tienen los tres ángulos iguales.

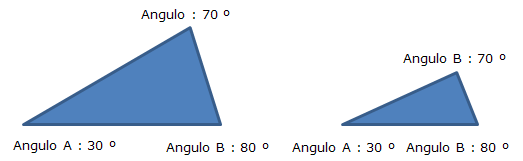
c) Un ángulo igual y los dos lados que se inician en dicho vértice son proporcionales

Estos dos ángulos tienen el ángulo C igual (30º) y los dos lados que se inician en dicho vértice son proporcionales.

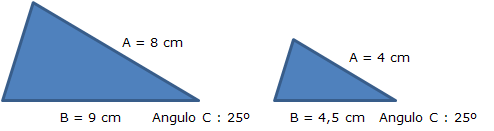
Lado A / Lado A’ = 8 / 4 = 2
Lado B / Lado B’ = 9 / 4,5 = 2

d) Dos triángulos en posición de Tales son semejantes

TRIÁNGULOS RECTÁNGULOS SEMEJANTES
Dos triángulos rectángulos son semejantes si cumplen alguna de las siguientes propiedades:

a) Tienen un ángulo agudo igual y uno de los catetos proporcionales

En ambos triángulos un lado agudo mide 40º. Como el ángulo recto mide 90º, el otro ángulo agudo tiene que medir 50º ya que en cualquier triángulo la suma de sus tres ángulos siempre es 180º.
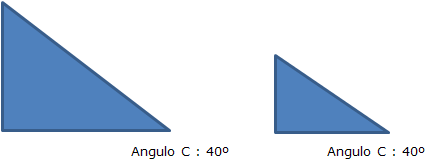
Por lo tanto los tres ángulos son iguales, que ya vimos antes que era uno de los requisitos para que dos triángulos fueran semejantes.

b) Tienen los dos lados catetos proporcionales

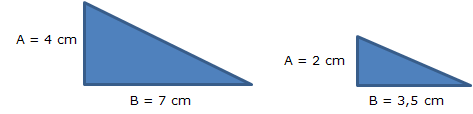
Lado A / Lado A’ = 4 / 2 = 2
Lado B / Lado B’ = 7 / 3,5 = 2

Al tener los dos lados catetos proporcionales, como el ángulo recto que forman mide 90º, cumple uno de los requisitos que vimos para que dos triángulos fueran semejantes.

c) Tienen un cateto y la hipotenusa proporcionales

Lado A / Lado A’ = 8 / 6 = 1,33
Lado B / Lado B’ = 4 / 3 = 1,33

Aplicando el Teorema de Pitágoras podemos calcular la longitud de los catetos que desconocemos.

Calculamos su proporción:

Lado C / Lado C’ = 6,928 / 5,196 = 1,33

Luego todos los lados son proporcionales que vimos que era uno de los requisitos para que dos triángulos fueran semejantes.




 Bibliográfica: http://www.aulafacil.com/Matematicas_2ESO/Curso/Lecc-22.htm