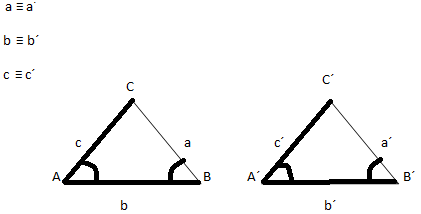
| TEOREMA DE PITÁGORAS |
En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
a2 + b2 = c2
| ||
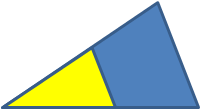
Cada uno de los sumandos, representa el área de un cuadrado de lado, a, b, c. Con lo que la expresión anterior, en términos de áreas se expresa en la forma siguiente:
| ||
El área del cuadrado construido sobre la hipotenusa de un triángulo rectángulo, es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.
| ||
Problemas:
1) Una ciudad se encuentra 17 km al oeste y 8 km al norte de otra. ¿Cuál es la distancia real lineal entre las dos ciudades?
2) Una escalera cuya longitud es de 3 metros se encuentra apoyada contra una pared en el suelo horizontal y alcanza 2,8 m sobre esa pared vertical. La pregunta es: ¿a qué distancia está al pie de la escalera de la base de la pared?
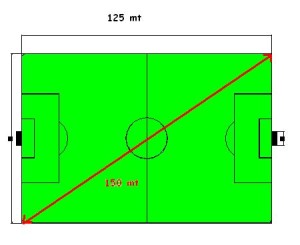
3) Una cáncha de fútbol (rectangular como sabemos) mide 125 metros de largo. Si la longitud de sus diagonales es de 150 metros. ¿cuál es el ancho del campo de juego?
Soluciones
1) Lo primero es realizar un pequeño dibujo que nos permita identificar la situación y ver cómo definimos un triángulo rectángulo en la misma.
Este podría ser un buen dibujo, donde observamos que se cumplen los datos que nos da el problema y que además la distancia real entre las ciudades, vendría a ser la hipotenusa de nuestro triángulo rectángulo.
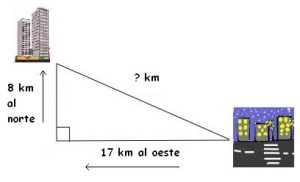 El triángulo entonces queda claramente definido y sabemos que tenemos un cateto que mide 17 km, otro que mide 8 km y que la distancia real que se nos está pidiendo es la hipotenusa del tal triángulo. Aplicamos Teorema de Pitágoras y el planteo sería así:
El triángulo entonces queda claramente definido y sabemos que tenemos un cateto que mide 17 km, otro que mide 8 km y que la distancia real que se nos está pidiendo es la hipotenusa del tal triángulo. Aplicamos Teorema de Pitágoras y el planteo sería así:
a2 = b2 + c2
a2 = 82 + 172 = 64 + 289 = 353
a = √353 = 18.8
a2 = 82 + 172 = 64 + 289 = 353
a = √353 = 18.8
Respuesta final: la distancia real entre las dos ciudades es de 18,8 km
2)
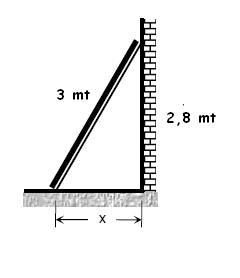 En este caso, el dibujo que podemos hacer para interpretar la letra del problema sería algo como esto, donde nuevamente se identifica sin problemas el triángulo rectángulo.
En este caso, el dibujo que podemos hacer para interpretar la letra del problema sería algo como esto, donde nuevamente se identifica sin problemas el triángulo rectángulo.
Queda claro que la escalera cumple el rol de la hipotenusa, la altura de la pared (dato conocido) es uno de los catetos y la distancia del pie de la escalera hasta la base de la pared, es el otro cateto, precisamente la medida que se nos pide calcular y que como es una incógnita para nosotros hemos llamado “x”.
El planteo de resolución en este caso podría ser el siguiente:
a2 = b2 + c2
32 = b2 + 2.82
9 = b2 + 7.84
b2 = 9 – 7.84 = 1.16
b = √1.16 = 1.08
32 = b2 + 2.82
9 = b2 + 7.84
b2 = 9 – 7.84 = 1.16
b = √1.16 = 1.08
Respuesta final: el pie de la escalera está a 1,08 mt de la pared.
3) Primer paso: la figura que ayuda a comprender
Analizando la figura, vemos que el triángulo queda comprendido por esa diagonal del campo de juego (la hipotenusa), el largo del campo (uno de los catetos) y el ancho (el otro cateto cuya longitud es lo que se nos pide hallar). El planteo de resolución sería el siguiente:
a2 = b2 + c2
1502 = 1252 + c2
22,500 = 15,625 + c2
c2 = 22,500 – 15,625 = 6,875
c = √6,875
1502 = 1252 + c2
22,500 = 15,625 + c2
c2 = 22,500 – 15,625 = 6,875
c = √6,875
c = 82.9
Respuesta final: el ancho del campo de fútbol es de 82,9 metros
Bibliografia: http://matematicasmodernas.com/problemas-resueltos-aplicando-teorema-de-pitagoras/#sthash.HOgTBxmw.dpuf






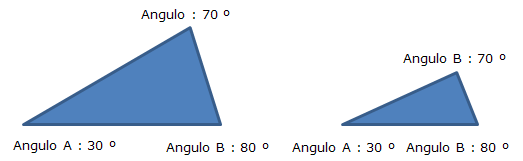
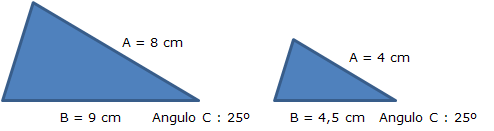
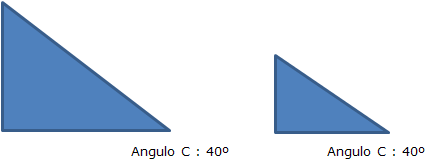
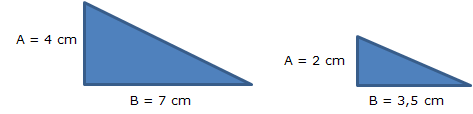


 Postulado ALA
Postulado ALA